La cryptographie derrière TLS : Les mécanismes de sécurité expliqués

Dans notre article précédent, nous avons introduit le protocole TLS et son importance pour la sécurité sur internet. Aujourd’hui, nous allons approfondir les mécanismes cryptographiques qui permettent à TLS de protéger vos données. Ces technologies complexes sont les fondations invisibles de la sécurité en ligne moderne.

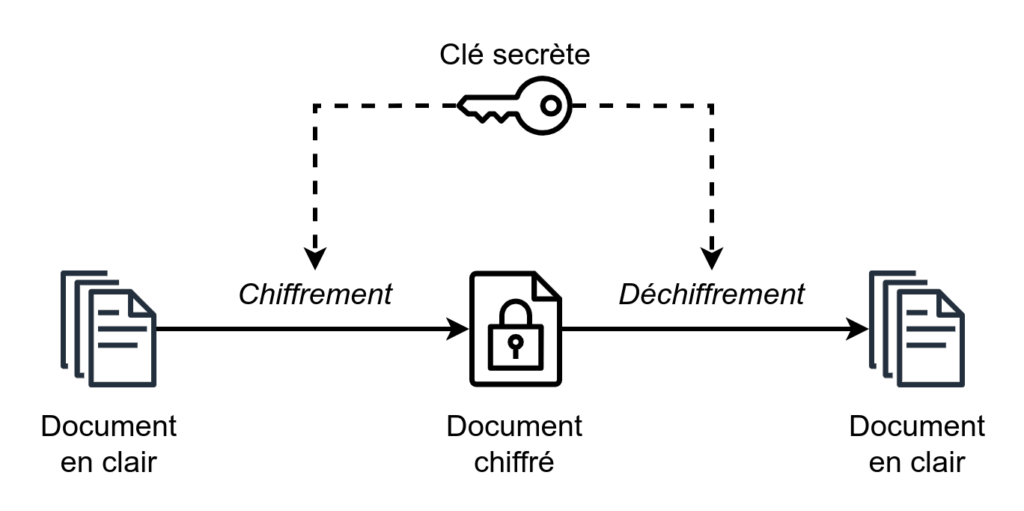
Le chiffrement symétrique

Le chiffrement symétrique utilise une seule clé de chiffrement pour sécuriser les communications. C’est la méthode privilégiée pour chiffrer de grandes quantités de données en raison de sa rapidité et de son efficacité.

Exemples courants :

• AES (Advanced Encryption Standard) : Utilisé pour sécuriser les communications gouvernementales et commerciales. Par exemple, quand vous naviguez sur votre banque en ligne, AES-256 (avec une clé de 256 bits) protège probablement vos données.
• ChaCha20 : Particulièrement efficace sur les appareils mobiles car il nécessite moins de puissance de calcul. Google l’utilise pour sécuriser de nombreuses connexions Chrome sur Android.

Le principal défi du chiffrement symétrique réside dans le partage sécurisé de la clé entre l’émetteur et le récepteur. Si un attaquant intercepte cette clé, toutes les communications peuvent être compromises.

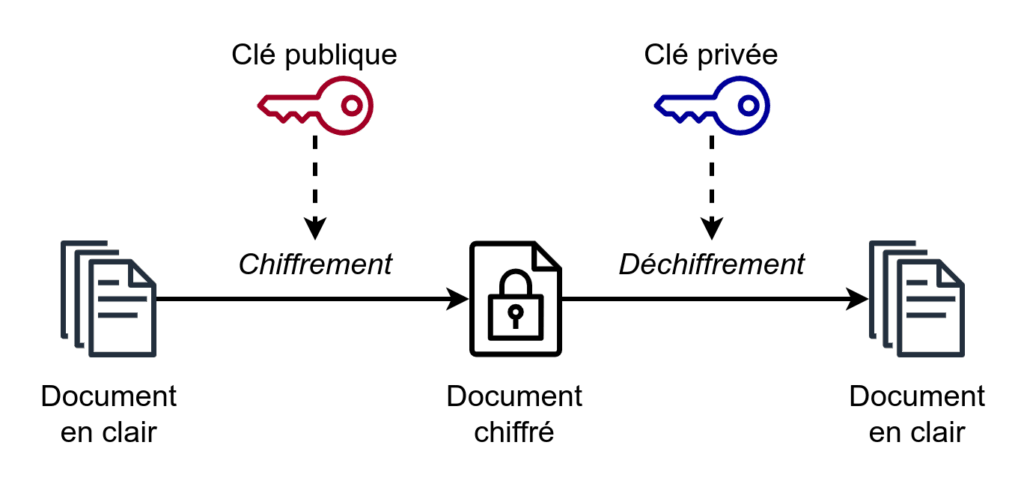
Le chiffrement asymétrique

Le chiffrement asymétrique résout le problème du partage de clés en utilisant une paire de clés mathématiquement liées :

• La clé publique peut être partagée avec tout le monde
• La clé privée reste strictement confidentielle

Ce système offre deux fonctionnalités fondamentales en fonction de la clé utilisée :

• Chiffrement : Une donnée chiffrée avec la clé publique ne peut être déchiffrée qu’avec la clé privée correspondante
• Signature : Une donnée signée (chiffrée) avec la clé privée peut être vérifiée (déchiffrée) par n’importe qui possédant la clé publique

Exemples pratiques :

• RSA : Largement utilisé pour les certificats TLS. Par exemple, quand Amazon vous présente son certificat, il utilise probablement RSA.
• ECDSA (Elliptic Curve Digital Signature Algorithm) : Plus efficient que RSA avec des clés plus courtes. Bitcoin utilise ECDSA pour signer les transactions.
• EdDSA (Edwards-curve Digital Signature Algorithm) : Utilisé par Signal et d’autres applications de messagerie sécurisée.

Bien que plus lent que le chiffrement symétrique, le chiffrement asymétrique est essentiel pour établir des communications sécurisées entre des parties qui n’ont jamais communiqué auparavant, et sert de fondation à la fois pour le partage sécurisé de clés et pour les mécanismes d’authentification comme les signatures numériques.

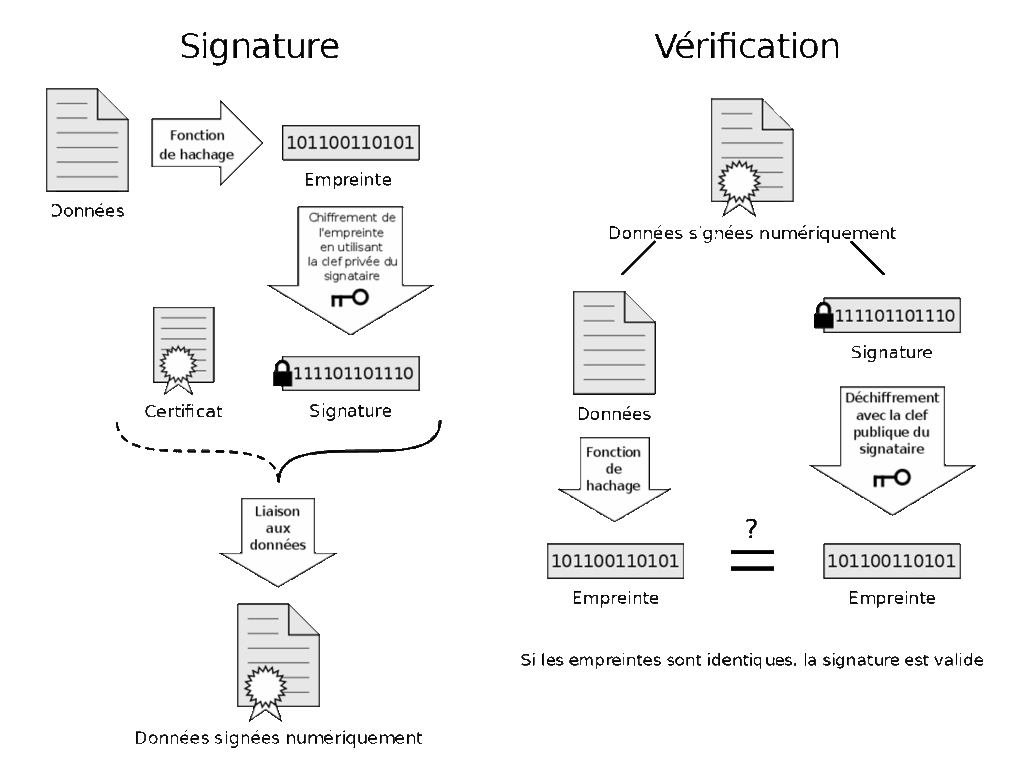
La signature numérique : le miroir du chiffrement asymétrique

La signature numérique représente l’utilisation inverse du chiffrement asymétrique, formant ainsi un tandem parfait pour la sécurité des communications. Alors que le chiffrement asymétrique classique utilise la clé publique pour chiffrer (seul le détenteur de la clé privée peut déchiffrer), la signature numérique utilise la clé privée pour signer (tout le monde peut vérifier avec la clé publique).

Cette inversion ingénieuse des rôles permet de garantir l’authenticité et l’intégrité d’un document ou d’un message. Voici comment cela fonctionne :

1. Création de l’empreinte : On utilise d’abord une fonction de hachage pour créer une empreinte unique (hash) du document à signer.
2. Signature avec la clé privée : Le signataire utilise sa clé privée pour chiffrer cette empreinte. C’est cette empreinte chiffrée qui constitue la signature numérique.
3. Vérification : Pour vérifier la signature, il faut :
   • Calculer l’empreinte du document reçu
   • Déchiffrer la signature avec la clé publique du signataire
   • Comparer les deux empreintes : si elles correspondent, la signature est valide

Illustration de la complémentarité :

• Pour le chiffrement : « Ce message est pour toi seul » (chiffré avec la clé publique du destinataire)
• Pour la signature : « Ce message vient bien de moi » (signé avec la clé privée de l’expéditeur)

Ces deux mécanismes peuvent être combinés pour obtenir à la fois confidentialité et authenticité : un message chiffré avec la clé publique du destinataire et signé avec la clé privée de l’expéditeur.

Ce système garantit deux choses essentielles :

• Authenticité : Seule la personne possédant la clé privée a pu créer cette signature
• Intégrité : Si le document a été modifié, même légèrement, l’empreinte calculée sera différente et la vérification échouera

Exemple concret : Lorsque vous téléchargez un logiciel comme Firefox, le fichier d’installation est accompagné d’une signature. Votre système vérifie cette signature avec la clé publique de Mozilla pour s’assurer que le fichier n’a pas été altéré et provient bien de Mozilla.

Dans le contexte de TLS, cette technique est utilisée pour :

• La signature des certificats par les autorités de certification
• La preuve de possession de la clé privée par le serveur lors du handshake
• La protection contre la modification des données en transit

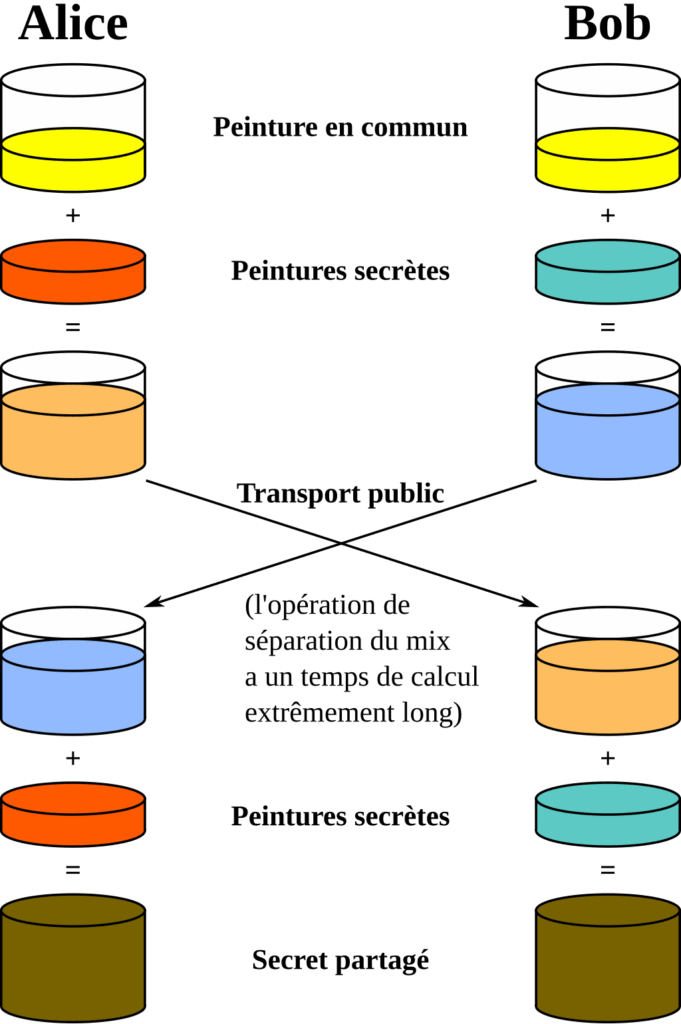
L’échange de clés Diffie-Hellman : un pont ingénieux

L’échange de clés Diffie-Hellman est une technique fondamentale permettant à deux parties de générer une clé secrète partagée en communiquant sur un canal non sécurisé, sans avoir besoin de s’échanger cette clé directement. Cette méthode élégante résout un problème crucial dans la cryptographie : comment partager un secret sans l’envoyer ?

Principe de fonctionnement :

1. Paramètres publics : Alice et Bob s’accordent sur deux nombres publics, généralement un nombre premier large (p) et une base (g).
2. Secrets individuels : Chacun génère un nombre secret personnel.
   • Alice choisit a et calcule A = g^a mod p
   • Bob choisit b et calcule B = g^b mod p
3. Échange public : Ils échangent uniquement leurs résultats A et B (pas leurs secrets a et b).
4. Calcul de la clé commune :
   • Alice calcule B^a mod p = (g^b)a mod p = g^(ab) mod p
   • Bob calcule A^b mod p = (g^a)b mod p = g^(ab) mod p

Les deux obtiennent le même résultat : g^(ab) mod p, qui devient leur secret partagé.

Sécurité : Un attaquant qui intercepte la communication ne voit que p, g, A et B. Pour trouver la clé commune, il devrait résoudre le « problème du logarithme discret » – un défi mathématique considéré comme pratiquement insoluble avec des nombres suffisamment grands.

Variantes modernes :

• ECDHE (Elliptic Curve Diffie-Hellman Ephemeral) : Une version utilisant les courbes elliptiques, offrant une sécurité équivalente avec des clés plus courtes. C’est aujourd’hui la méthode privilégiée dans TLS 1.3.
• DHE (Diffie-Hellman Ephemeral) : Version où de nouvelles clés sont générées à chaque session (éphémères), garantissant une « forward secrecy » – même si une clé privée est compromise plus tard, les sessions passées restent protégées.

Exemple concret : Quand vous vous connectez à votre webmail sécurisé, votre navigateur et le serveur utilisent probablement ECDHE pour établir une clé de session unique. Cette clé ne sera jamais transmise sur le réseau et sera oubliée après votre déconnexion, rendant impossible le déchiffrement ultérieur de vos communications, même si les clés à long terme du serveur sont compromises.

Dans TLS, l’échange Diffie-Hellman est typiquement utilisé conjointement avec les certificats. Le certificat authentifie le serveur, puis l’échange DH permet d’établir une clé de session unique pour chiffrer la communication.

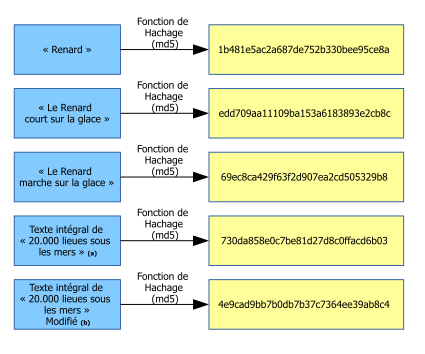
Les fonctions de hachage

Les fonctions de hachage sont des algorithmes qui transforment des données de taille arbitraire en une empreinte de taille fixe. Ces empreintes sont essentielles pour vérifier l’intégrité des données.

Exemples courants :

• SHA-256 : Utilisé dans Bitcoin pour sécuriser la blockchain. Si vous avez déjà vérifié un téléchargement important en comparant des « checksums », vous avez probablement utilisé SHA-256.
• SHA-3 : La version plus récente et encore plus sécurisée de SHA, utilisée dans des systèmes nécessitant une haute sécurité.
• BLAKE3 : Une fonction de hachage très rapide utilisée dans certains systèmes de stockage distribué.

Les fonctions de hachage présentent plusieurs propriétés importantes :

• Il est pratiquement impossible de retrouver les données d’origine à partir de l’empreinte
• Deux documents différents ont une probabilité extrêmement faible de produire la même empreinte
• Une modification minime dans le document d’origine change complètement l’empreinte

Ces propriétés font des fonctions de hachage des outils indispensables pour vérifier l’intégrité des données et créer des signatures numériques.

L’interaction des mécanismes de sécurité dans TLS

Le génie de TLS réside dans sa façon de combiner ces différentes techniques cryptographiques pour tirer parti des avantages de chacune :

1. Le chiffrement asymétrique est utilisé pour l’authentification et l’échange initial de clés, où sa robustesse compense sa lenteur relative
2. Le chiffrement symétrique prend ensuite le relais pour la communication continue, offrant performance et sécurité
3. L’échange Diffie-Hellman permet l’établissement sécurisé d’une clé de session unique, offrant une confidentialité persistante même en cas de compromission future
4. Les fonctions de hachage et signatures numériques garantissent l’authenticité et l’intégrité tout au long du processus

C’est cette combinaison intelligente qui permet à TLS d’offrir une sécurité maximale tout en restant suffisamment rapide pour une utilisation quotidienne.

Conclusion

Ces mécanismes cryptographiques forment l’épine dorsale de la sécurité en ligne moderne. Bien que techniquement complexes, leur interaction dans le protocole TLS permet de sécuriser nos communications de manière transparente et efficace.

Dans notre prochain article, nous explorerons les certificats TLS – ces « cartes d’identité numériques » qui permettent d’authentifier les sites web et d’établir la confiance en ligne.

Continuez à suivre notre série d’articles sur le protocole TLS pour découvrir les certificats, l’établissement des connexions sécurisées et la gestion pratique avec OpenSSL.